二维空间中的准粒子由于其绕行路径所具有的拓扑特性，因此可以满足不同于玻色子和费米子的任意子统计规律。任意子又可分为阿贝尔任意子和非阿贝尔任意子，其中满足非阿贝尔统计的任意子可以通过粒子空间位置的交换（编织）而演化为一个新的量子态。基于这种奇异特性，研究者们希望将信息编码在非阿贝尔任意子中，并通过非阿贝尔任意子的编织操作实现信息的处理和运算，即“拓扑量子计算”。由于拓扑的保护，拓扑量子计算具有包括可容错性在内的一系列优点，因而业已成为量子计算中备受关注的重要分支。

过去约二十年间针对拓扑量子计算的研究主要集中于Majorana零模（或者手性Majorana边态）。Majorana粒子的反粒子是其本身，其在凝聚态物理体系中的实现依赖于超导序参量的存在。最近，565net必赢客户端量子材料科学中心博士生吴宜家（现为565net必赢客户端博雅博士后）在导师谢心澄院士的指导下，与江华（苏州大学）、刘杰（西安交通大学）、刘海文（北京师范大学）合作，提出了在狄拉克费米子模这一非Majorana体系（非超导体系）中实现非阿贝尔编织的方案，相关论文已于近日在线发表于《物理评论快报》［Physical Review Letters125, 036801.https://link.aps.org/doi/10.1103/PhysRevLett.125.036801］。

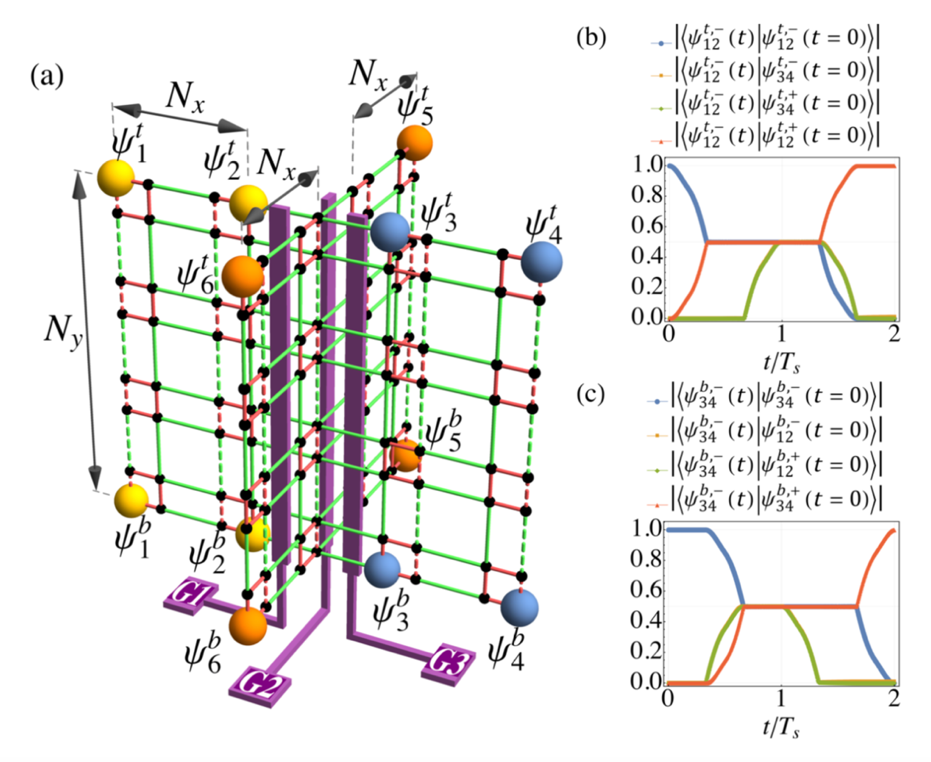
(a)实现非阿贝尔编织的高阶拓扑绝缘体纳米结构的示意图；(b), (c)非阿贝尔编织过程中的波函数演化。

狄拉克费米子模在凝聚态物理中的典型例子是拓扑绝缘体中受拓扑保护的零能边缘态，近年来广受关注的高阶拓扑绝缘体中的拓扑角态便是一类典型的狄拉克费米子模。通过对拓扑角态编织过程中的波函数演化进行数值模拟，谢心澄研究组证明了拓扑角态所具有的非阿贝尔编织特性。在数值计算之外，该工作还解析研究了二维拓扑绝缘体中的半整数磁通涡旋所束缚的狄拉克费米子模，该束缚模与拓扑角态在拓扑起源和数学形式上均高度相似。通过对相应波函数演化的解析描述，磁通涡旋束缚的狄拉克费米子模的非阿贝尔编织特性同样可以得到证明，且不难发现其非阿贝尔特性与拓扑所引起的几何相位紧密相关。

上述结果表明，在非Majorana体系（非超导体系）中，受到拓扑保护的狄拉克费米子模同样也可以展现出非阿贝尔编织效应。与Majorana零模相比，狄拉克费米子模在Fock空间中具有不同的量子维度，且其编织算符和编织矩阵的形式也与Majorana零模不同。实验上，基于狄拉克费米子模的非阿贝尔编织具有无需超导序参量、能隙较大、编织耗时短等优点，且有望在一维Su-Schrieffer-Heeger链、高阶拓扑绝缘体等体系中得以实现。因此，该研究为非阿贝尔编织乃至拓扑量子计算的实现提供了新的思路。

该工作得到了国家自然科学基金的资助。